Lazy and infinite data structures

Most of the times, we face problems where the solutions can be expressed as simple IO functions. Given an input the answer to the problem can be determined by following a step by step algorithm.

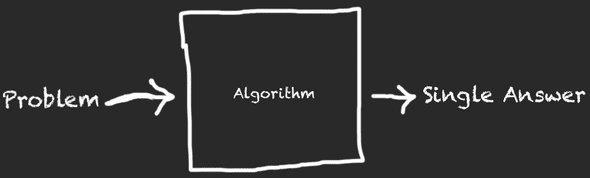
There are cases though, that there are multiple answers to our problem, or the solutions’ space is just not finite (or seem to not be finite). Sometimes, even if the solution can be found operating on finite sets, is more elegant to write our algorithm by imagining that we operate in the infinite space of possible solutions.

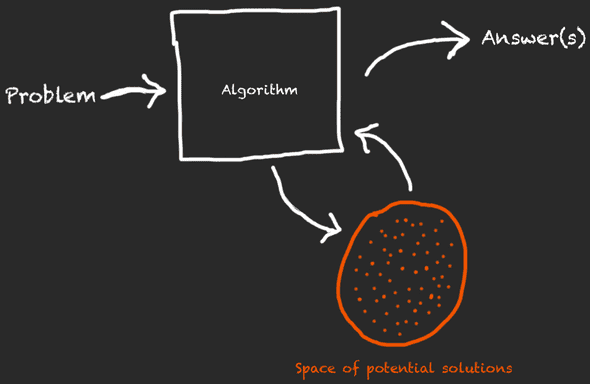
What I mean by “a more elegant way” is that many times, is more readable to express the control flow of an algorithm with high level abstractions instead of low level primitives.

High Level Abstractions	Low level primitives
`map`, `filter`	`if`, `while`

The problem is that high level abstractions have their own cost, and certain limitations. For example in Javascript map creates a new intermediate array every time it is chained, and it requires to know the size of the iterable in advance.

Saying that we can be more elegant operating on the infinite space, may sound weird but in reality we do it all the time in our daily life. As long as an infinite construction is finitely describable, we can easily reason about it. Examples of these kind of constructions are:

Sets of strings over some alphabet
The set of all positive integers
Functions that map items between sets

Imagine that we have a list of 100000 integers [1,2,3,4,5,6, ... 100000] and we want to find the first 2 of them that satisfy a certain expression (and the calculation of that expression is time consuming). We could write that in a functional style

const satisfies = [1,2,3,4,5,6, ... , 100000]
  .map(heavyCalculation)
  .filter(satisfiesCondition)
  .slice(0, 2);

There are a few problems in this approach:

We calculate the result of heavyCalculation even if we don’t need it, e.g. if 1,2 already satisfy our requirements.
Every chain, has to re-iteratare the whole array.
As mentioned, in JS specifically every time you use .map a new intermedidate array is created, wasting memory.
We need to know or construct the array beforehand.

Let’s see how we can define a data structure, that express the infinite space of positive integers, avoid calculating the whole space of possible solutions and avoid wasting memory (by not creating intermediate iterables).

First lets define a data structure that represents all the positive integers:

class PositiveIntegers {
  constructor() {
    this.index = 1;
  }

  [Symbol.iterator](){ return this; }

  next() {
    while (true) {
      return { done: false, value: this.index++ }
    }
  }
}

Implementing the Symbol.iterator and next let us conform with the iterator protocol and do things like:

const positives = new PositiveIntegers();

for(let k of positives){
  console.log(k) // prints  1,2,3,4... for ever
}

Although we can use for ... of we cannot use .map since PositiveIntegers do not support it. Let’s define another high abstraction, an interface that express the mapping operation over the infinite space.

class InfiniteMap {
  constructor(iterable, callback) {
    this.iterable = iterable;
    this.callback = callback;
  }

  [Symbol.iterator](){ return this; }

  next() {
    const item = this.iterable.next();
    const mappedValue = this.callback(item.value);
    return { value: mappedValue, done: item.done };
  }
}

It accepts an iterable and loop forever on it calling a callback. Then we can define the map function of PositiveIntegers in terms of InfiniteMap.

class PositiveIntegers {
  constructor() {
    this.index = 1;
  }

  [Symbol.iterator](){ return this; }

  next() {
    while (true) {
      return { done: false, value: this.index++ }
    }
  }

  map(callback) {
    return new InfiniteMap(this, callback);
  }
}

This let us do things like:

const positives = new PositiveIntegers();
const mapFn = i => i * 5;

const mappedList = positives.map(mapFn);

for(let k of mappedList){
  console.log(k);
}

We are now able to overcome the limitations of the native .map and travel over an infinite set. Let’s see how we travel over the infite and stop when we find the “solution” we are looking for.

class InfiniteUntil {
  constructor(iterable, callback) {
    this.iterable = iterable;
    this.callback = callback;
  }

  [Symbol.iterator]() { return this; }

  next() {
    const item = this.iterable.next();

    if (this.callback(item.value)) { // stop the iteration
      return { done: true };
    }

    return { value: item.value, done: item.done };
  }
}

And use it in our main data structure:

class InfinitePositives {
  constructor() {
    this.index = 1;
  }

  [Symbol.iterator]() { return this };

  next() {
    while (true) {
      return { done: false, value: this.index++ };
    }
  }

  map(callback) {
    return new InfiniteMap(this, callback);
  }

  takeUntil(callback){
    return new InfiniteUntil(this, callback);
  }
}

This let us do things like:

const positives = new PositiveIntegers();
const untilFn = i => i > 20;
const positivesUntilTwenty = positives.takeUntil(untilFn);

for(let k of positivesUntilTwenty){
  console.log(k); // will print 1..20
}

There is a problem though. We cannot chain the functions of PositiveIntegers

We can’t do:

positives.map(mapFn).takeUntil(untilFn);

positives.takeUntil(untilFn).map(mapFn);

Since map returns InfiniteMap which does not implement the takeUntil, and takeUntil returns InfiniteUntil which does not implement map.

We can fix that by using our PositiveIntegers as base and extend.

We define our InfiniteMap and InfiniteUntil by extending PositiveIntegers. Inside PositiveIntegers we define map and takeUntil using InfiniteMap and InfiniteUntil.

Putting everything together:

class InfinitePositives {
  constructor(iterable, callback) {
    this.index = 1
    this.iterable = iterable || this;
    this.callback = callback || ((i) => i);
  }

  [Symbol.iterator]() { return this; }

  next() {
    while (true) {
      return { done: false, value: this.index++ }
    }
  }

  map(callback) {
    return new InfiniteMap(this, callback);
  }

  takeUntil(callback){
    return new InfiniteUntil(this, callback);
  }
}

class InfiniteMap extends InfinitePositives {
  next() {
    const item = this.iterable.next();
    const mappedValue = this.callback(item.value);
    return { value: mappedValue, done: item.done };
  }
}

class InfiniteUntil extends InfinitePositives {
  next() {
    const item = this.iterable.next()

    if (this.callback(item.value)) { // stop the iteration
      return { done: true }
    }

    return { value: item.value, done: item.done }
  }
}

And now we can chain our map and takeUntil functions

const mapFn = i => i * 5
const untilFn = i => i > 20

const list = new InfinitePositives()

for (const k of list.map(mapFn).takeUntil(untilFn)) {
  console.log(k); 
}

We don’t have to always pass a callback, we can define take that stops after specific number of steps.

class InfiniteTake extends InfinitePositives {
  constructor(iterable, steps) {
    super(iterable);
    this.steps = steps;
    this.index = 0;
  }

  next() {
    const item = this.iterable.next()

    if (this.index === this.steps) { // stop the iteration
      return { done: true }
    }

    this.index++;

    return { value: item.value, done: item.done }
  }
}

class InfinitePositives {
  constructor(iterable, callback) {
    this.index = 1
    this.iterable = iterable || this;
    this.callback = callback || ((i) => i);
  }

  [Symbol.iterator]() { return this }

  next() {
    while (true) {
      return { done: false, value: this.index++ }
    }
  }

  map(callback) {
    return new InfiniteMap(this, callback);
  }

  take(steps){
    return new InfiniteTake(this, steps);
  }

  takeUntil(callback){
    return new InfiniteUntil(this, callback);
  }
}

This essentially means that

for (const k of list.take(5).map(mapFn)) {
  console.log(k)
}

is equal to

for (const k of list.map(mapFn).take(5)) {
  console.log(k)
}

We can also defined the each to abstract the for .. of loop.

class InfinitePositives {
  constructor(iterable, callback) {
    this.index = 1
    this.iterable = iterable || this
    this.callback = callback || (i => i)
  }

  [Symbol.iterator]() { return this }

  next() {
    while (true) {
      return { done: false, value: this.index++ }
    }
  }

  map(callback) {
    return new InfiniteMap(this, callback)
  }

  take(size) {
    return new InfiniteTake(this, size)
  }

  takeUntil(callback) {
    return new InfiniteUntil(this, callback)
  }

  each(callback) {
    for(let item of this){
      callback(item);
    }
  }
}

So we can write

list.take(5).map(mapFn).each(console.log)

We created a new data structure that express the infinite set of all positive integers. What if we want to express another infinite set, e.g. the Fibonacci Set, or the set of Negative Even Numbers, and we want to use the same functions we defined for the PositiveIntegers ?

We can create a new interface that supports the ability to operate on infinity sets. Let’s call it InfinitySupport

let InfiniteMap, InfiniteTake, InfiniteUntil;

class InfinitySupport {
  constructor(iterable, callback) {
    this.iterable = iterable || this;
    this.callback = callback || (i => i);
  }

  [Symbol.iterator]() { return this; }

  next() {
    throw Error('next() should be overwritten by the subclass')
  }

  map(callback) {
    return new InfiniteMap(this, callback);
  }

  take(size) {
    return new InfiniteTake(this, size);
  }

  takeUntil(callback) {
    return new InfiniteUntil(this, callback);
  }

  each(callback) {
    for (const item of this) {
      callback(item);
    }
  }
}

InfiniteMap = class _InfiniteMap extends InfinitySupport {
  next() {
    const item = this.iterable.next();
    const mappedValue = this.callback(item.value);
    return { value: mappedValue, done: item.done };
  }
}


InfiniteUntil = class _InfiniteUntil extends InfinitySupport {
  next() {
    const item = this.iterable.next();

    if (this.callback(item.value)) { // stop the iteration
      return { done: true };
    }

    return { value: item.value, done: item.done };
  }
}

InfiniteTake = class _InfiniteTake extends InfinitySupport {
  constructor(iterable, size) {
    super(iterable);
    this.size = size;
    this.index = 0;
  }

  next() {
    const item = this.iterable.next();

    if (this.index === this.size) { // stop the iteration
      return { done: true };
    }

    this.index++;

    return { value: item.value, done: item.done };
  }
}

Then we can define our sets in relation to that:

class InfinitePositives extends InfinitySupport {
  constructor(iterable, callback) {
    super(iterable, callback);
    this.index = 1;
  }

  next() {
    while (true) {
      return { done: false, value: this.index++ };
    }
  }
}

class FibonaciNumbers extends InfinitySupport {
  constructor(iterable, callback) {
    super(iterable, callback);
    this.previousprevious;
    this.previous = 0;
    this.current = 1;
  }

  next() {
    while (true) {
      this.previousprevious = this.previous;
      this.previous = this.current;
      this.current = this.previous + this.previousprevious;
      return { done: false, value: this.current };
    }
  }
}

class NegativeEvenIntegers extends InfinitySupport {
  constructor(iterable, callback) {
    super(iterable, callback);
    this.start = 0;
  }

  next() {
    while (true) {
      return { done: false, value: (this.start = this.start - 2) };
    }
  }
}

And use the functions we defined in the InfinitySupport

const fibo = new FibonaciNumbers();

fibo.take(5).each(console.log);

const negativeEven = new NegativeEvenIntegers();

negativeEven.take(5).each(console.log);

So what did we achieved?

We raised the level of abstraction, by chaining high order concepts.
We avoid storing intermediate representations, and hence waisting memory.
We don’t operate on the whole set, but we are lazily evaluate on step at a time.

Laziness

In the previous examples, we defer the calculation of a value (the execution of our callback), until we need it. Lazy evaluation usually is combined with memoization. After a value is computed the result is stored in a cache, the next time the calculation is requested, the function returns the stored value instead of computing it again.

We can implement a LazyArray data structure, that supports .map in a lazy way, and avoids re-calculation using memoization.

class LazyMap {
  constructor(iter, callback) {
    this.iter = iter;
    this.callback = callback;
    this.calculatedValues = {};
  }

  [Symbol.iterator](){
    return this;
  }

  next(){
    const item = this.iter.next();

    if(!item.done) {

      if(this.calculatedValues[item.value] !== undefined) {
        return { done: item.done, value: this.calculatedValues[item.value] }
      }
  
      this.calculatedValues[item.value] = this.callback(item.value)
  
      return { done: item.done, value: this.calculatedValues[item.value] }
    }

    return { done: true }
  }
}

class LazyArray {
  constructor(arr) {
    this.arr = arr;
    this.index = 0;
  }

  [Symbol.iterator](){
    return this;
  }

  next(){
    while(this.index !== this.arr.length) {
      return { done: false, value: this.arr[this.index++] };
    }
    return { done: true, value: this.arr[this.index] };
  }

  map(callback) {
    return new LazyMap(this, callback);
  }
}

Inside our LazyMap we use a cache to ensure that the callback doesn’t run for the same input more than once.

For example executing the following:

const arr = new LazyArray([3,4,6,7,3,4,6]);

const callback = function(i){
  console.count(`Called for ${i}`);
  return i * 10;
}

const p = arr.map(callback);

for(let k of arr.map(callback)){
  console.log(k);
}

Gives us

Called for 3: 1
30
Called for 4: 1
40
Called for 6: 1
60
Called for 7: 1
70
30
40
60

The callback function has been invoked only once per uniq input value.

Problems that can be expressed more elegantly

Imagine that we have to implement the game of chess. The possible games are not infinite:

Number of moves	Number of possible games
1	20
2	400
3	8,902
4	197,281
5	4,865,609
6	119,060,324
7	3,195,901,860
8	84,998,978,956
9	2,439,530,234,167
…	…

… but probably if we had to model that, would be easier to imagine that they are.

Problems that can be expressed as decision trees are also good candidates for the use of infinite data structures, specially when the nodes of the tree cannot be determined beforehand but we build the tree as we go.

For example if we had a problem that can be expressed as decision tree and we know that each node can have maximum 3 leaves.

We can create a lazy data structure that would allow us to model that:

class TriTree {
  constructor(value, left, middle, right) {
    this.value = value;
    this.left = left;
    this.middle = middle;
    this.right = right;
  }

  * [Symbol.iterator]() {
    yield this.getValue();

    if (this.left) {
      yield* this.left;
    }
    if (this.middle) {
      yield* this.middle;
    }
    if (this.right) {
      yield* this.right;
    }
  }

  getValue() {
    // we could have complex calculations, and memoization here
    return this.value;
  }
}

For example this tree:

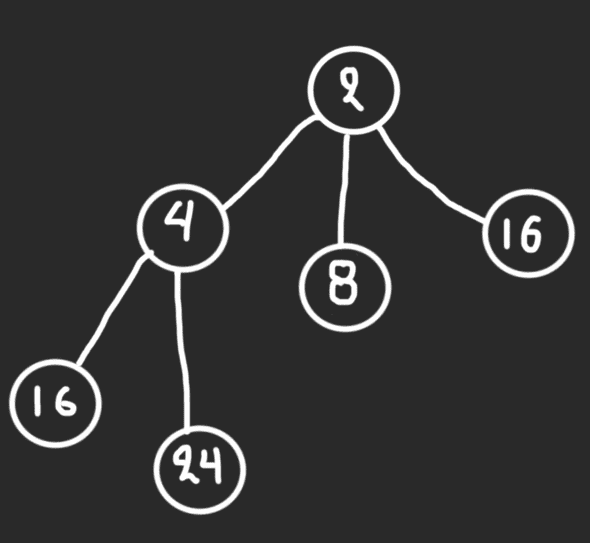
could be written like:

const t = new TriTree(
  2,
  new TriTree(
    4,
    new TriTree(
      16,
    ),
    new TriTree(
      24,
    ),
  ),
  new TriTree(
    8,
  ),
  new TriTree(
    16,
  ),
);

Summary

There are certain problems that can be easier model if we imagine that we operate on the infinite space, (even if we don’t). Examples:

Read line by line from a file where we don’t know then number of lines
Streams of data in a message bus
Problems that can be expressed as decision trees
Problems that involve permutations or combinations of finite sets

And others that by definition we have to model infinite sets. Being able to model that in high order abstractions, gives us the power to write cleaner and more performant programs (using lazy evaluation and memoization techniques).

Published 12 Jul 2019

Engineering Manager. Opinions are my own and not necessarily the views of my employer.
Avraam Mavridis on Twitter